Séries chronologiques stellaires des Champs Profonds
Cette page présente une série photométrique temporelle de 28108 sources ponctuelles situées dans les Champ Profonds de la CFHTLS. Les quatre secteurs des Champ Profonds de la CFHTLS ont fait l'objet d'observations régulières depuis le début de 2003, d'abord dans le cadre de la CFHTLS proprement dite, ensuite pour l'étalonnage des étoiles standard au CFHT. Toutes les données de la CFHTLS sont aujourd'hui du domaine public et les images étalonnées des étoiles standard le deviennent la nuit même de l'étalonnage. Avec des données s'étalant sur dix ans, les Champ Profonds est ensemble de données de grande valeur pour l'étude des étoiles variables.
Méthode
En résumé, la série temporelle a été produite comme suit:
- Sélection: Un catalogue des sources ponctuelles présentes dans le champ profond a été créé.
- Photométrie d'ouverture: Pour chaque source et pour chaque image, la photometrie à travers des d'ouverture réglée au seeing a été effectuée.
- Correction des points zéro: Les magnitudes ont fait l'objet de petites corrections au point zéro sur chaque image.
- Erreurs photométrique: Les incertitudes photométriques (limités par les erreurs de calibration) ont été calculés
- Complétude: la complétude a été évaluée dans chaque bande.
- Diffusion: Téléchargez les données
Sélection des sources ponctuelles
La liste d'étoiles est extraite des piles de "meilleures seeing" venant des Champs Profonds, dont on trouvera une description détaillée ici. Brièvement, il s'agit d'images obtenues par co-addition des images de la meilleure qualité prises dans le champ profond. La visibilité est de 0.65" pour toutes les piles des bandes GRIZ et de 0.8" pour celles de la bande U. L'image de la bande G sert d'image de référence. Le locus stellaire a été identifié sur un graphique opposant la largeur à mi-hauteur (FWHM) et la magnitude, comme on peut le voir ci-dessous. Ici, la FWHM a été établie d'après le rayon de demi-lumière en pixels, que l'on a multiplié par 0.32 pour obtenir la FWHM en secondes d'arc.
La figure ci-dessous montre le locus stellaire d'un secteur des Champ Profonds. Du côté le plus lumineux, le relèvement de la FWHM indique qu'on approche de la saturation; du côté le moins lumineux, le locus stellaire se confond avec les galaxies compactes. Le critère retenu pour peupler le catalogue était 17.5>G>24 et FWHM=0.65 +/- 15%, comme l'indiquent les lignes rouges.
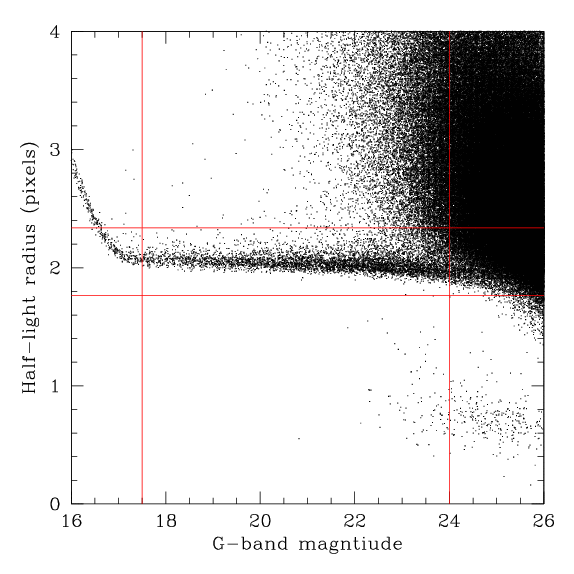
Photométrie d'ouverture
On a appliqué la photométrie d'ouverture à chaque source ponctuelle sur chacune des 11765 images disponibles dans le champ profond de la CFHTLS. On a recouru à l'étalonnage astrométrique avec MegaPipe pour convertir la position des objets, exprimée en RA et en Dec, en une position exprimée par un nombre secondaire et en pixels (X,Y). La position des objets a été précisée davantage par application d'une fonction gaussienne à la FWHM de l'image. Ce recentrage décale habituellement la position de l'objet de 0.1 pixel (ou 0.02 seconde d'arc).
Le niveau du fond de ciel a été établi au moyen d'un anneau d'un rayon intérieur de 70 pixels et d'un rayon extérieur de 90 pixels. La figure ci-dessous représente une étoile brillante. La fonction d'étalement (PSF) donne un centre lumineux entouré d'un disque clair plus ténu, aux bords bien définis. Selon l'emplacement de l'étoile dans la mosaïque, il est rare que l'image de la pupille soit centrée sur l'étoile. Le rayon intérieur de 70 pixels fait en sorte que le disque des images de la pupille ne se situe pas à l'intérieur de l'anneau.

L'étape suivante consiste à appliquer la photométrie d'ouverture à chaque source en recourant à une série d'ouvertures. Plusieurs types d'ouverture peuvent être utilisés. Le champ profond de la CFHTLS a été étalonné avec la fonction MAG_AUTO de SExtractor, qui est une ouverture Kron à magnitude variable. Cette fonction donne les meilleurs résultats avec les galaxies et ne convient pas nécessairement aux étoiles. Il est préférable d'utiliser une ouverture à diamètre fixe, mais la seeing des images de la CFHTLS varie considérablement, si bien qu'il y aura fluctuation de la quantité de lumière qui traverse l'ouverture. Si l'ouverture est assez grande pour que les effets résultant de la visibilité soient négligeables, l'image inclura une trop grande partie du ciel et l'erreur attribuable au hasard sera plus importante. Pour éviter cela, il faut corriger l'ouverture en fonction de l'infini. Enfin, on peut recourir à une ouverture par visibilité/concordance comme le suggèrent Regnault et al. (2009) Dans ce cas, l'ouverture est un multiple de la qualité de l'image (IQ). La méthode a pour avantage d'autoriser des ouvertures relativement petites qui capteront une fraction cohérente de la lumière, ce qui élimine la nécessité d'une correction. C'est cette méthode qui a été retenue. Une question demeure: quel multiple de l'IQ devrait-on utiliser? Les multiples de 1 à 9 ont été testés, puis on a corrigé le point zéro et l'ouverture tel qu'indiqué ci-dessous. La dispersion photométrique de chaque objet a été établie. Les objets ont été regroupés par magnitude et on a calculé la médiane de la dispersion.
La figure ci-dessous montre la dispersion photométrique selon la magnitude, l'ouverture et le filtre. Pour les sources les plus lumineuses, on obtient généralement la dispersion la plus faible avec une ouverture égale au quadruple de la seeing. Pour les objets plus faible, la dispersion augmente de façon monotone avec l'ouverture. Une ouverture égale au quadruple de la visibilité a été retenue pour obtenir la meilleure photométrie possible avec les objets brillants.
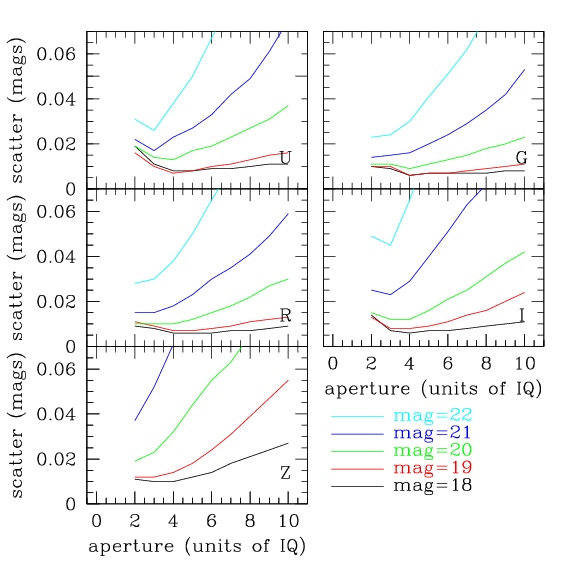
La photométrie d'ouverture a été réalisée avec le système de traitement CANFAR. On a recouru pour cela à la trousse de photométrie d'ouverture IRAF. Le champ profond n'est pas surencombré. Par conséquent ajuster la photométrie avec la FEP (par ex. DAOphot) ne présente aucun avantage sensible.
Correction des ouvertures/points zéro
L'étalonnage photométrique des Champs Profonds de la CFHTLS a été effectué avec la fonction MAG_AUTO de SExtractor. MAG_AUTO est une magnitude Kron, principalement employée pour la photométrie des galaxies. Elle crée une ouverture elliptique d'après les moments de deuxième ordre de la source. Plus celle-ci est étendue, plus grande sera l'ouverture. L'ouverture négligera toujours une petite (2%) fraction de la lumière émise par la source, quelle qu'en soit l'étendue. S'il s'agit de toute évidence d'un avantage pour la photométrie des galaxies, on estime généralement que cela pose un inconvénient pour la photométrie des étoiles, ce qui explique pourquoi on a préféré recourir à la photométrie d'ouverture pour le projet.
La conversion entre la photométrie d'ouverture et MAG_AUTO nécessite une correction. Il s'avère que si l'ouverture est un multiple d'IQ (plutôt qu'un nombre fixe de secondes d'arc), la correction prend une valeur assez uniforme. On mesure le décalage du point zéro pour chacune des 11765 images prises dans le champ profond, puis on compare la magnitude de l'ouverture établie avec les images aux valeurs MAG_AUTO venant des piles d'images. Seules les étoiles qui apparaissent sur toutes les images dans le secteur du champ profond pour un filtre particulier sont utilisées pour la comparaison. On corrige le point zéro et l'ouverture en appliquant le principe du scepticisme artificiel (Stetson, 1989) de manière à rejeter les aberrations attribuables aux rayons cosmiques ou aux colonnes défectueuses. Le diagramme ci-dessous présente les résultats de cette correction:
La figure ci-dessous montre l'écart entre les points zéro obtenus avec MAG_AUTO et avec la magnitude (ouverture) d'après l'ouverture, pour l'ensemble des images regroupées par filtre. Quand l'ouverture ne correspond qu'au double d'IQ, la correction est de l'ordre de +0.2 magnitude (MAG_AUTO capte plus de lumière que la magnitude de l'ouverture).Du côté de l'ouverture la plus large, la correction est de -0.05 magnitude. Soulignons que la courbe n'a pas encore totalement atteint un plateau.
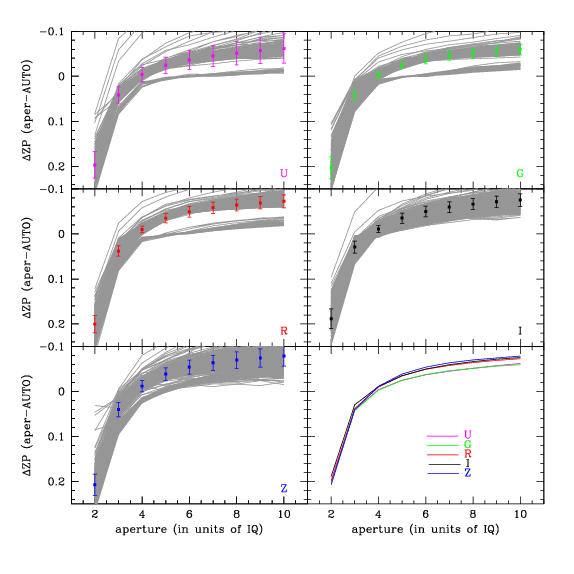
Les courbes en gris représentent des images individuelles. Les points de couleur et les barres d'erreur correspondent à la moyenne et à l'écart-type de chaque ouverture. Les plupart des filtres révèlent deux locus distincts. Les images situées dans le locus inférieur ont été prises lors de deux rondes d'observation en 2007, époque où, semble-t-il, la FEP avait un profil sensiblement différent. On compte 10 à 20 images dans ce locus, comparativement aux quelque 2000 groupées dans le locus principal. Hormis ces exceptions peu nombreuses, MAG_AUTO s'avère une excellente valeur de remplacement pour les ouvertures appariées à l'IQ.
Sur le panneau inférieur droit, on peut voir les corrections moyennes apportées à tous les filtres sur le même diagramme.
La figure ci-dessous montre la variation de la correction du point zéro en fonction de l'IQ. Elle trace l'écart entre la valeur calculée par MAG_AUTO et la magnitude mesurée avec une ouverture quatre fois plus grande que l'IQ, séparée par un filtre. Chaque filtre présente une légère pente, mais la différence entre IQ=0.5" et IQ=1" varie de 0.001 à 0.0045 magnitude, soit un peu moins que la dispersion usuelle de 0.005 magnitude. Le nouveau et l'ancien filtre I apparaissent sur le même tracé, ce qui explique la dispersion légèrement plus élevée. La distribution semble aussi légèrement bimodale: la tache inférieure correspond au nouveau filtre I. Encore une fois, il semble que MAG_AUTO soit une excellente valeur de remplacement pour l'ouverture appariée à l'IQ dans diverses conditions de visibilité.
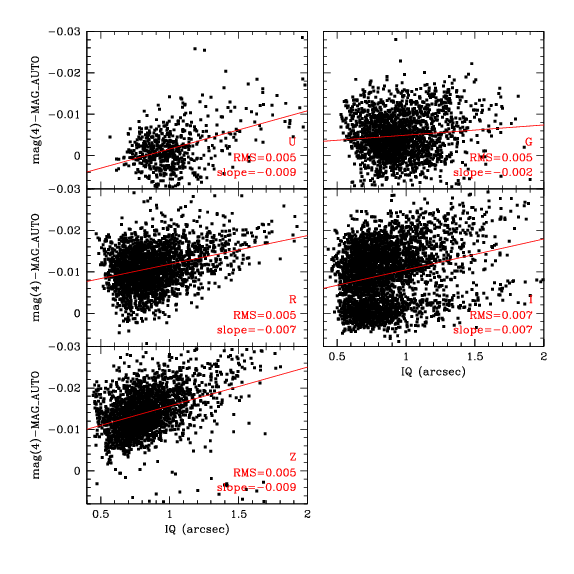
Ces corrections ont été apportées à chaque image et sont disponibles sous forme de fichier ASCII (DeepVarZPAP.gz).
Erreurs photométriques
IRAF calcule les incertitudes photométriques d'après le bruit de lecture du détecteur ainsi que le bruit poissonien du ciel et de l'objet. Cependant, on a constaté que la dispersion photométrique s'avérait considérablement plus importante que celle illustrée uniquement par le bruit de Poisson, surtout quand la luminosité est plus grande.
C'est ce qu'illustre la figure ci-dessous. Les points correspondent à la différence absolue entre la magnitude d'une image et le flux mesuré dans la pile. La ligne rouge indique l'erreur médiane en fonction de la magnitude; la verte, l'erreur médiane d'après la magnitude calculée par IRAF, c'est-à-dire en tenant compte des parasites de lecture et du bruit poissonien. Du côté où la luminosité est la plus vive, l'écart se chiffre à environ 0.01 magnitude pour cette image, mais il fluctue d'une image à l'autre.
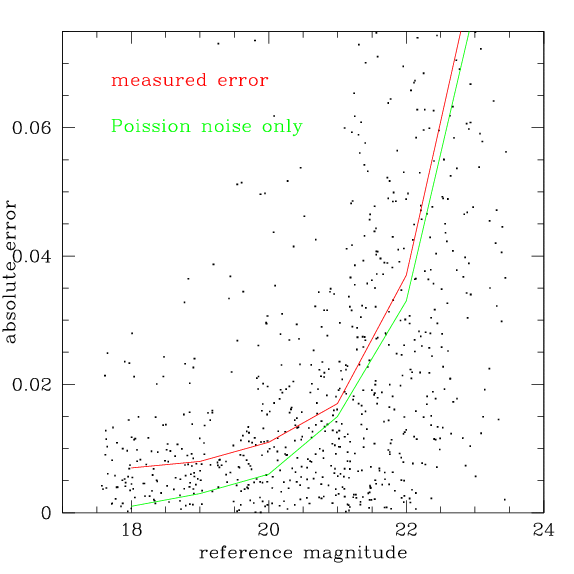
La différence a son importance. On aimerait mesurer la plus petite variation de luminosité possible et il est malheureux qu'on ne puisse obtenir mieux que 1% avec la magnitude, même quand elle est élevée.
D'autres chercheurs n'ont pas réussi à obtenir mieux avec la photométrie des images de MegaCam. Bien que l'équipe de la SNLS ait enregistré une photométrie de qualité supérieure à 1% après avoir combiné plusieurs images, et que leur étalonnage du point zéro ait une précision supérieure à 1%, quand on compare les mesures prises individuellement sur les étoiles brillantes d'une image à l'autre, on remarque habituellement une dispersion de 2% (Fabbro, communication personnelle). Stetson (communication personnelle) estime qu'il faut ajouter une erreur de 1% à la quadrature des incertitudes de Poisson pour tenir compte de la dispersion.
Après avoir examiné soigneusement les erreurs possibles au niveau de la détermination du point zéro et les corrections à apporter à l'ouverture dont il est question plus haut, on en est parvenu à la conclusion que les erreurs pourraient survenir lorsqu'on procède à l'élimination des tendances avec Elixir. Les images présentant un écart supérieur à l'écart usuel entre l'erreur de Poisson et l'erreur mesurée ont été examinées à l'oeil nu. Ces images présentaient manifestement un problème soit au niveau de la bordure (dans la bande Z), soit au niveau du champ plat. Des exemples suivent.
Le problème que soulève cette image de la bande Z résulte d'une mauvaise soustraction des franges d'interferances.

Cette image présente des variations évidentes du fond sous forme de bandes horizontales.

Ici la difficulté est plus subtile, mais un examen attentif révèle des motifs en arrière-plan. Il s'agit d'une image de la bande G et il ne s'agit pas de franges d'interferances.

On en conclut ceci: bien que les erreurs du champ plat soient trop faibles pour que l'oeil les perçoive dans la plupart des cas, elles existent néanmoins et expliquent la limite de 0.01 pour l'erreur au niveau de la magnitude.
L'erreur de magnitude indiquée dans les tableaux de distribution a été modifiée en conséquence. L'erreur reposant sur la médiane est mesurée à intervalles de 1 magnitude sur chaque image. Elle correspond à la ligne rouge sur la figure ci-dessus. Les erreurs indiquées dans les tableaux ont été interpolées linéairement à partir de ces valeurs. Les valeurs de IRAF ont été conservées quand la magnitude était inférieure à 22.
Complétude
Les étoiles ne sont pas toutes visibles sur chaque image. Les images ont été prises avec des décalages. Celles à la bordure du capteur pourraient donc se trouver totalement hors de ce dernier, sur une autre image, c'est-à-dire dans l'espace séparant les puces, ou à l'extérieur de la surface que représente l'image. Les étoiles moins luisantes pourraient ne pas être détectées sur une image prise dans des conditions où la visibilité était piètre, où la transparence laissait à désirer ou lorsque le ciel était trop clair.
La figure ci-dessous montre la fraction récupérée en fonction de la magnitude et du filtre. Par récupération, on entend un objet qui a été détecté et dont l'incertitude photométrique est inférieure à 0.1 magnitude. Soulignons qu'il est impossible de parvenir à une absolue complétude (100%) en raison des décalages.
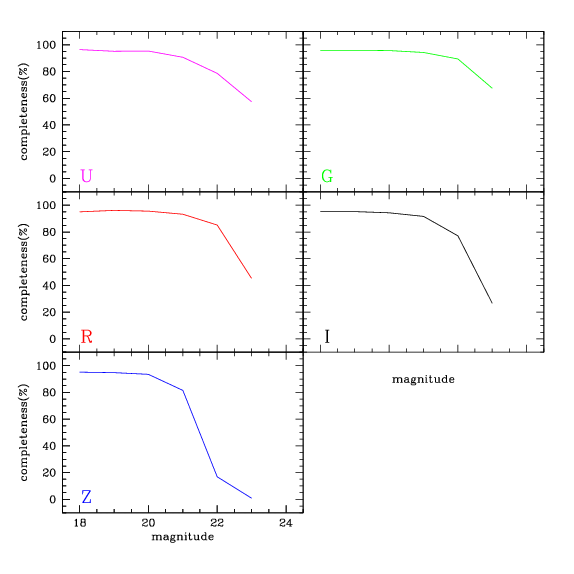
Diffusion
La série temporelle est disponible sous la forme de deux archives tar (tarball) de 28108 fichiers, à raison d'un fichier par étoile. Les fichiers sont en langage ASCII ordinaire et comptent une rangée par image. L'image est omise quand on n'y détecte pas d'objet, soit parce qu'il n'y en avait pas dans le capteur, soit parce qu'il luisait trop faiblement. Par conséquent les fichiers n'ont pas tous la même taille. Il existe deux jeux de fichiers.
-
DeepVarTerse.tar.gz (625Mb):
Ces fichiers ne renferment que ce qui suit:
- Point milieu de l'exposition (MJD)
- Magnitude
- Incertitude pour cette magnitude
-
Chiffre correspondant au filtre:
- 1: U
- 2: G
- 3: R
- 4: I
- 5: I2
- 6: Z
-
DeepVarFull.tar.gz (2.7Gb):
Ces fichiers fournissent un peu plus de précisions. Chaque
fichier comprend un en-tête donnant la magnitude UGRIZ de
l'objet dans la pile ainsi que des liens menant aux parties
découpées autour de chaque objet, dans les piles. Chaque entrée
comprend des informations supplémentaires avec lesquelles on
peut retracer la position d'un objet inhabituel sur une image
donnée, puis remonter jusqu'aux photons d'origine.
- Numéro de l'exposition MegaCam
- Nombre de l'extension de où l'objet a été détecté
- Coordonnées X et Y en pixels dans cette image
- Qualité de l'image en secondes d'arc de l'image
- Filtre sous forme de lettre (UGRIZ et I2)
- Lien vers une des zones découpées autour de l'objet original
- Date de modification :