Le samedi 24 janvier 2026, à partir de 8h (Pacific), les services de CANFAR et du CCDA pourraient subir des pannes ou des interruptions temporaires en raison d'une maintenance planifiée. La maintenance durera au moins 24h et se terminera le dimanche 25 janvier matin.
Vérifications du profondeur
Cette page décrit la série de vérifications qui sont faites dans WIRwolf à veiller à ce que la profondeur totale est atteinte. La profondeur de chaque image d'entrée est calculée en ajoutant des faux étoiles et en mesurant le taux de récupération en fonction de la grandeur. Ces profondeurs sont convertis en un temps d'exposition efficace. La somme des durées d'exposition efficace de l'ensemble des images est ensuite reconverti en une profondeur prévue qui est comparé à la profondeur réelle mesurée sur chaque image.
La limite de complétude de 50% est adoptée comme mesure de la profondeur. Il est mesurée par en effectant des découpes de l'image contenant les étoiles lumineuses. Ces timbres-poste sont mises à l'échelle des magnitudes de plus en plus faibles et rajoutées à l'image. SExtractor est exécuté sur l'image pour voir si les étoiles peuvent être récupérés.
Dans les champs encombrés, les sources ajoutées sont dans a possibilté de ne pas être recuperés non pas parce qu'ils sont trop faibles, mais parce qu'ils se posent sur véritable source. Pour tenir compte de cette possibilité, les sources de l'image sont masqués et remplacés par des pixels ayant les mêmes propriétés de bruit que le ciel. Les étoiles sont ajoutés et récupérés et la limite de 50%-complétude est mesurée comme avant. Ce limite (généralement plus profond) est appelée la limite d'image vide.
Le graphique ci-dessous montre un exemple. Dans ce cas, la limite de la complétude de 50% est K = 20.1, comme indiqué par la ligne rouge. Dans cette image assez vide, à la limite de l'image vide n'est que légèrement plus profond, comme indiqué par la ligne bleue.
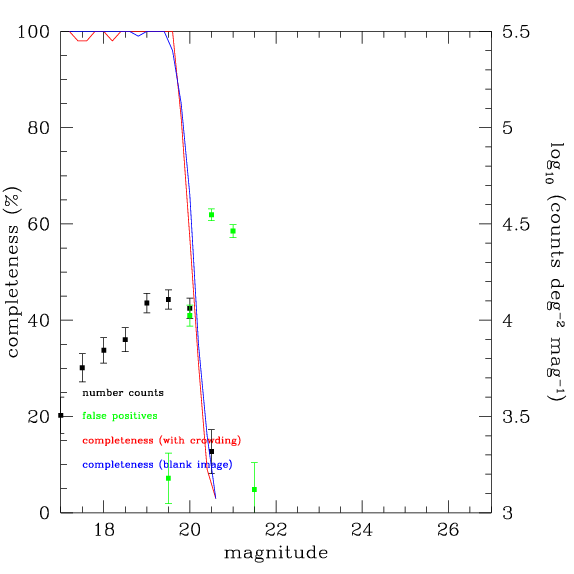
Des contrôles supplémentaires sont présentés sur ce graphique. Les points noirs avec des barres d'erreur indiquent le histogramme des détéction des source. Les points verts indiquent le taux de faux positifs. L'image est multipliée par -1 et SExtractor est tournée que comme avant. Toutes les sources détectées sont, bien sûr, les faux positifs. Les faux positifs deviennent plus nombreux que les véritables sources à peu près la même grandeur que la limite de 50%.
La magnitude limite croît avec la durée d'exposition comme:
magnitude limite = 1.25*log (temp de pose) + constante
Bien sûr, d'autres facteurs influencent la profondeur: facteurs atmosphériques tels que le seeing, la transparence et la luminosité du ciel par exemple. Mais nous pouvons définir un temps d'exposition effective, le teff en inversant l'équation ci-dessus. Cette teff n'aura qu'une relation faible à la durée d'exposition réelle, mais elle inclut les facteurs atmosphériques. Par conséquent, la somme des teffs des images d'entrée dans une image empilé devrait être un meilleur indicateur de la profondeur que la somme des temps d'exposition réel, car elle reflète les variations des conditions atmosphériques.
La valeur exacte de la constante dans l'équation ci-dessus n'est pas pertinent pour le calcul actuel, car il se pris en compte à la fin. Mais pour les images WIRCAM il est d'environ 19,0
Dans l'exemple actuel, il y avait 15 images d'entrée, avec des profondeurs efficaces allant de 20.0 à 20.5. Si la valeur de la constante est de 19.0 magnitudes que nous avons:
10**((20.1 - 19.0)/1.25) = 10.1 10**((20.1 - 19.0)/1.25) = 10.1 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.0 - 19.0)/1.25) = 8.0 10**((20.1 - 19.0)/1.25) = 10.1 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.5 - 19.0)/1.25) = 25.3 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7
Additionnant les temps d'exposition que nous obtenons 200,5, pour une profondeur prévue de
1.25*log (200.5) + 19.0 = 22.5
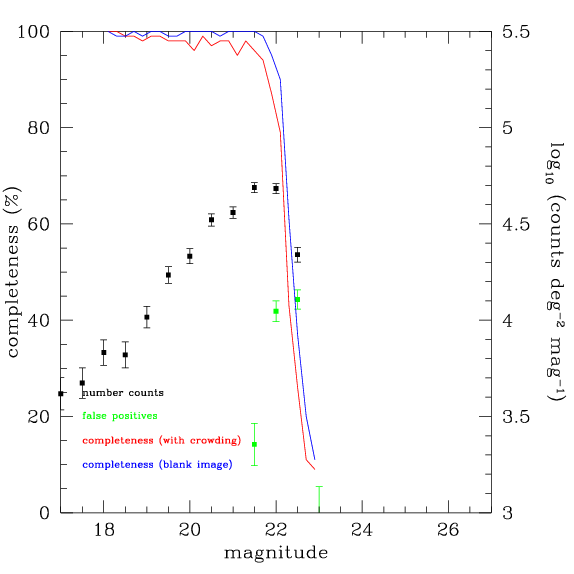
La profondeur de l'image empilé est mesurée d'une manière similaire, en ajoutant faux étoile à l'image de sortie, comme indiqué ci-dessous. Dans ce cas, la profondeur mesurée est de K = 22.4, à proximité de la profondeur prévue de 22.5
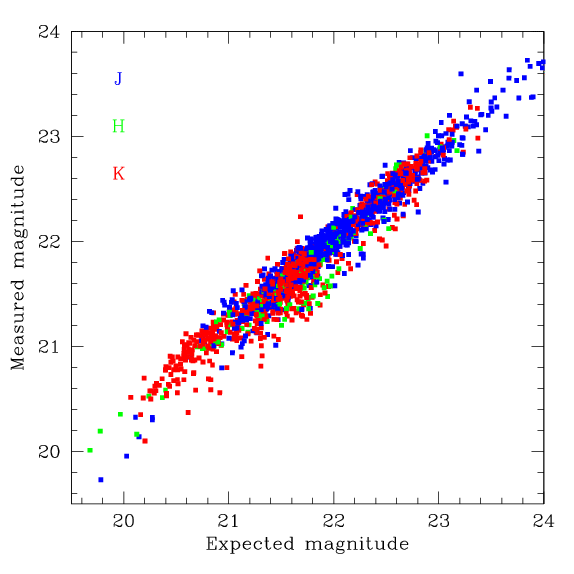
En général, il ya une certaine dispersion sur la relation entre la profondeur mesurée et de la profondeur attendue comme le montre la figure ci-dessous. Toutefois, ce graphique indique que la profondeur est bien préservé par le processus d'empilement WIRwolf.
- Date de modification :