Checks on depth
This page describes the series of checks that are done in WIRwolf to ensure that the full depth is reached. The depth of each input image is computed by adding fake stars and measuring the recovery rate as a function of magnitude. These depths are converted into an effective exposure time. The sum of the effective exposure times of all the images is then converted back into an expected depth which is compared to the actual depth measured on each image.
The 50% completeness limit is adopted as the metric of depth. It is measured by excising subrasters of the image containing bright stars. These postage stamps are scaled to fainter and fainter magnitudes and added back to the image. SExtractor is run on the image to see if the stars can be recovered.
In crowded fields, the added sources stand a chance of being missed not because they are too faint, but because they land on real source. To account for this possibility, the sources in the image are masked and replaced with pixels with the same noise properties as the sky. Stars are added and recovered and the 50%-completeness limit is measured as before. This (generally deeper) limit is referred to as the blank image limit.
The plot below shows an example. In this case the 50% completeness limit is K=20.1, as shown by the red line. In this fairly empty image, the blank image limit is only marginally deeper, as shown by the blue line.
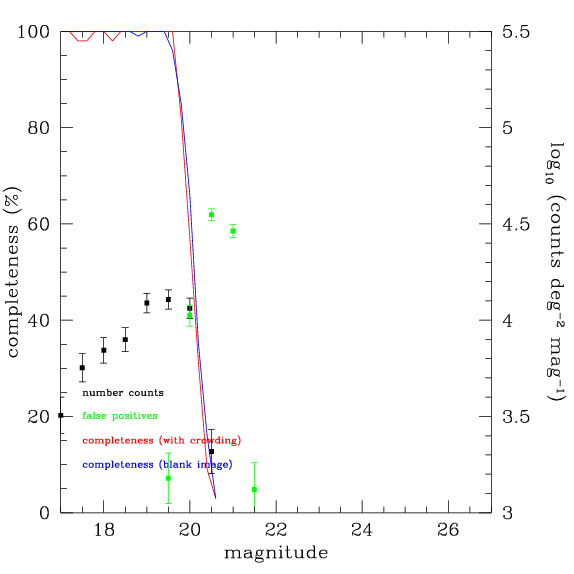
Additional checks are shown on this plot. The black points with error bars show the source number counts. The green points show the false positive rate. The image is multiplied by -1 and SExtractor as run as before. All sources detected are, of course, false positives. The false positives become as numerous as the real sources at roughly the same magnitude as the 50% limit.
The magnitude limit scales with exposure time as:
magnitude limit = 1.25*log (exposure time) + constant
Of course other factors influence the depth: atmospheric factors such as seeing, transparency and sky brightness for example. But we can define an effective exposure time, teff by inverting the above equation. This teff will have only a tenuous relationship to the real exposure time, but has folded into it the atmospheric factors. Therefore the sum of the teffs of the input images in an image stack should be an better indicator of depth than the sum of the real exposure times, because it will reflect the variations in atmospheric conditions.
The exact value of the constant in the equation above is irrelevant for the current calculation since it gets factored out at the end. But for WIRcam images it is approximately 19.0
In the current example, there were 15 input images, with effective depths ranging from 20.0 to 20.5. Taking the value of the constant to 19.0 magnitudes we have:
10**((20.1 - 19.0)/1.25) = 10.1 10**((20.1 - 19.0)/1.25) = 10.1 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.0 - 19.0)/1.25) = 8.0 10**((20.1 - 19.0)/1.25) = 10.1 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.5 - 19.0)/1.25) = 25.3 10**((20.3 - 19.0)/1.25) = 16.0 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7 10**((20.2 - 19.0)/1.25) = 12.7
Summing the exposure times we get 200.5, for an expected depth of
1.25*log (200.5) + 19.0 = 22.5
The depth of the stack is measured in a similiar way, by adding fake stars to the output image, as shown below. In this case the measured depth is K=22.4, close to the expected depth of 22.5
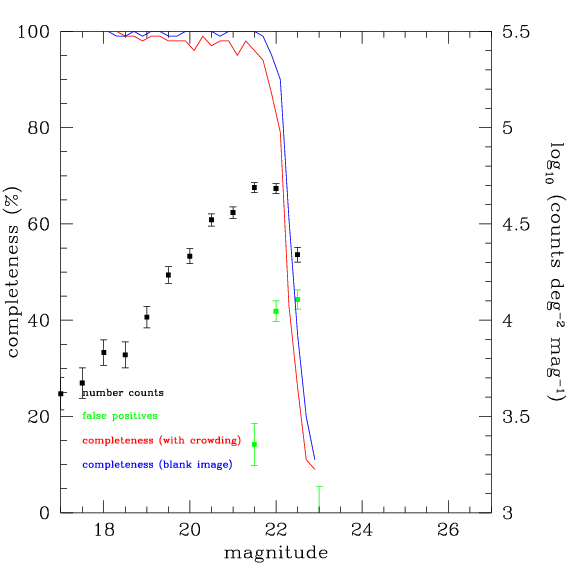
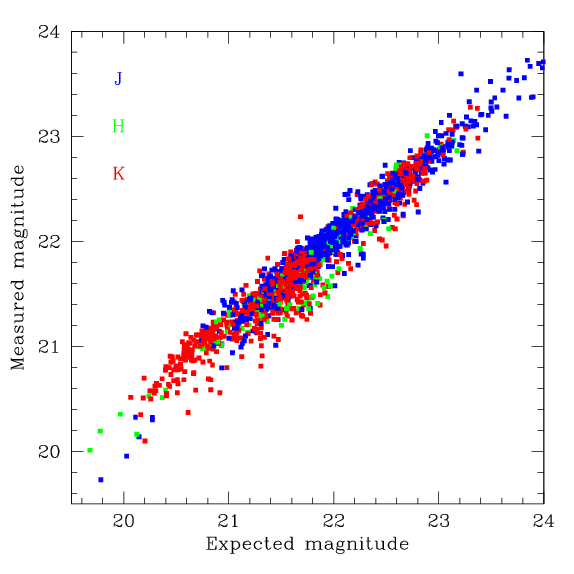
In general, there is some scatter about the relation between measured depth and expected depth as shown by the figure below. However, this plot indicates that depth is properly being preserved by the WIRwolf stacking process.
- Date modified: